Accelerated Time Flow at Cosmic Extremes

Title: Accelerated Time Flow at Cosmic Extremes: A Novel Explanation for Early Galaxy

Formation

Authors: Pastor John L McGary, Dr. Isabella M Kay, Ludlow research center, Ludlow Maine

Abstract:

Observations from the James Webb Space Telescope (JWST) have identified galaxies at high

redshifts that appear more developed than predicted by standard cosmological models. This

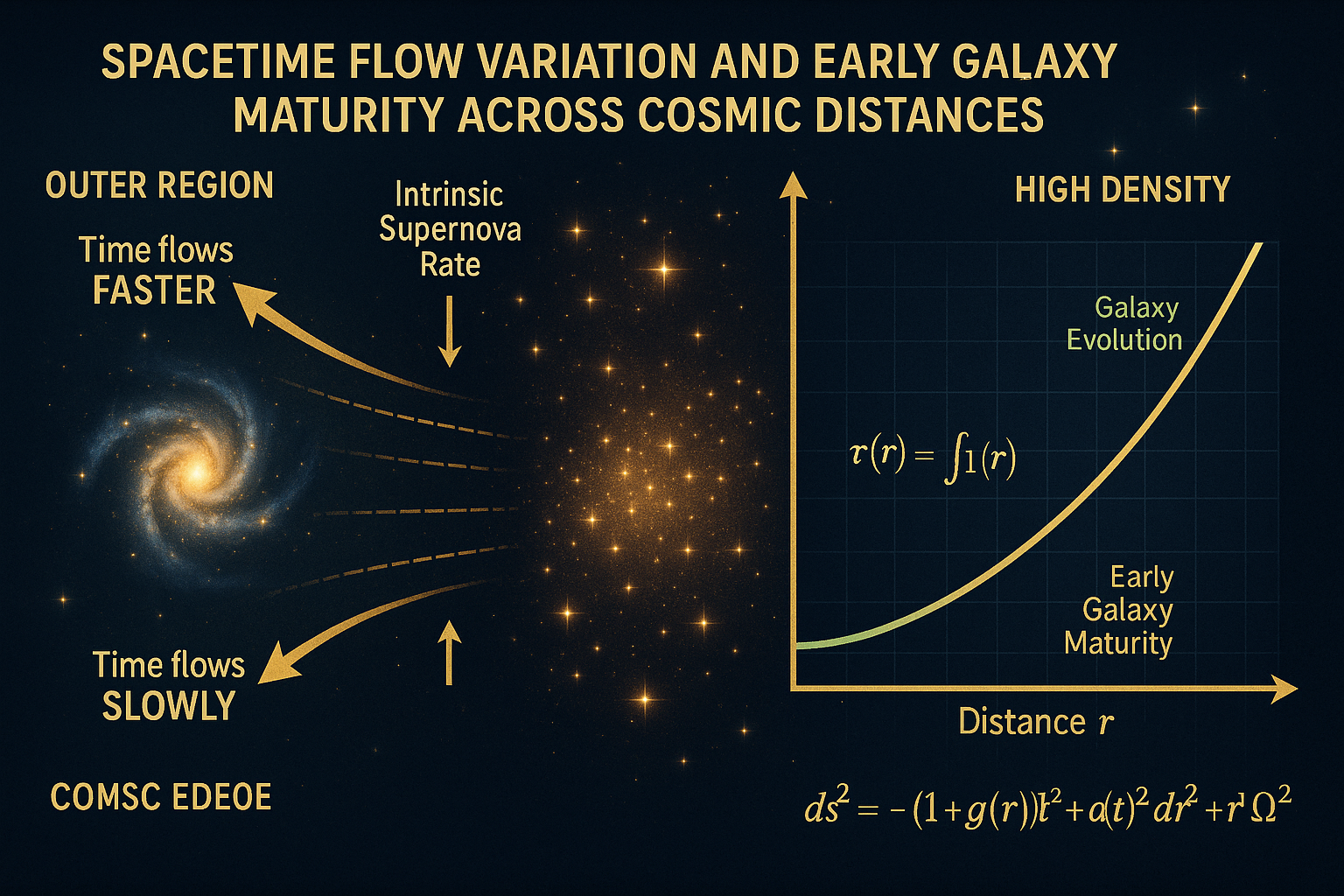
paper proposes that time flows faster near the edge of the universe due to lower mass

density, an inverse effect of gravitational time dilation. We develop a modified cosmological

framework to incorporate this hypothesis and explore its implications for structure formation.

The model predicts an increased rate of supernova discharges in distant galaxies, providing a

testable signature for future observations.

Introduction

The Lambda Cold Dark Matter (ΛCDM) model has long served as the cornerstone of modern

cosmology, successfully describing phenomena from the cosmic microwave background to

galaxy clustering.[^1] However, recent JWST observations have revealed galaxies at redshifts

z>10z > 10z > 10

with unexpectedly mature characteristics, such as high stellar masses and advanced

morphologies, challenging the timelines of standard structure formation.[^2] These findings

suggest that galaxy evolution may have occurred more rapidly than anticipated in the early

universe.

In general relativity, time dilation near massive objects slows the passage of time relative to

regions of lower gravitational potential.[^3] This principle implies that in areas with minimal

mass, time should flow faster. If the universe possesses an "edge"—or regions of significantly

reduced density—time could accelerate there, potentially resolving the JWST anomaly. This

paper introduces a theory positing that time flows faster closer to the cosmic periphery,

accelerating the development of early galaxies. We present a modified cosmological model

and propose an observational test involving supernova rates in high-redshift galaxies.

Theoretical Framework

Gravitational Time Dilation and Its Inverse

Einstein’s theory of general relativity establishes that the rate of time is influenced by

gravitational potential. The proper time

τ\tau\tau

for an observer in a gravitational field is:

dτ=1−2GMc2r dtd\tau = \sqrt{1 - \frac{2GM}{c^2 r}} \, dtd\tau = \sqrt{1 - \frac{2GM}{c^2

r}} \, dt

where ( G ) is the gravitational constant, ( M ) is the mass, ( c ) is the speed of light, ( r ) is the

radial distance, and ( dt ) is the coordinate time.[^4] In regions far from mass, where

2GMc2r≈0\frac{2GM}{c^2 r} \approx 0\frac{2GM}{c^2 r} \approx 0

,

dτ≈dtd\tau \approx dtd\tau \approx dt

, suggesting a faster flow of time. We hypothesize that near the "edge" of the universe—

defined here as regions of minimal mass density—time flows more rapidly than in denser

areas.

A Modified Cosmological Metric

Standard Friedmann-Lemaître-Robertson-Walker (FLRW) cosmology assumes homogeneity

and isotropy, with no spatial variation in time flow.[^5] To accommodate our theory, we

propose a modified metric inspired by inhomogeneous models like the Lemaître-Tolman-

Bondi (LTB) framework.[^6] Consider a metric:

ds2=−(1+g(r))dt2+a(t)2dr2+r2dΩ2ds^2 = -\left(1 + g(r)\right) dt^2 + a(t)^2 dr^2 + r^2

d\Omega^2ds^2 = -\left(1 + g(r)\right) dt^2 + a(t)^2 dr^2 + r^2 d\Omega^2

where ( a(t) ) is the scale factor, ( r ) is the radial coordinate, and ( g(r) ) is a function that

increases with distance, reflecting lower density at larger ( r ). For comoving observers, the

proper time is:

dτ=1+g(r) dtd\tau = \sqrt{1 + g(r)} \, dtd\tau = \sqrt{1 + g(r)} \, dt

If

g(r)>0g(r) > 0g(r) > 0

at large ( r ),

dτ>dtd\tau > dtd\tau > dt

, meaning time flows faster in these regions. The effective age of the universe at position ( r )

becomes:

τ(r)=∫0t1+g(r) dt′>t\tau(r) = \int_0^t \sqrt{1 + g(r)} \, dt' > t\tau(r) = \int_0^t \sqrt{1 +

g(r)} \, dt' > t

This increased proper time allows distant regions to experience more evolutionary history for

a given cosmic time ( t ).

Implications for Early Galaxy Formation

In the ΛCDM model, galaxy formation proceeds via the hierarchical growth of density

perturbations, paced by cosmic time ( t ).[^7] Our model introduces a spatial variation in time

flow, such that galaxies near the cosmic edge (observed at high ( z )) have greater

τ\tau\tau

than their ( t ) suggests. This accelerated timeline permits more rapid star formation and

structural development.

JWST data reveal galaxies at

z≈12z \approx 12z \approx 12

with stellar masses exceeding

109M⊙10^9 M_\odot10^9 M_\odot

and significant metal enrichment, implying formation within the first 300 million years post-Big

Bang.[^8] In our framework, these galaxies, located at large ( r ), have experienced a proper

time

τ(r)\tau(r)\tau(r)

substantially greater than the cosmic time ( t ) at their redshift, enabling their precocious

maturity.

Predictions: Supernova Rates as a Test

Our theory predicts observable effects in the supernova rates of distant galaxies. In standard

cosmology, the observed rate

RobsR_{\text{obs}}R_{\text{obs}}

of supernovae is diluted by cosmological time dilation:

Robs=Rintrinsic1+zR_{\text{obs}} = \frac{R_{\text{intrinsic}}}{1 + z}R_{\text{obs}} =

\frac{R_{\text{intrinsic}}}{1 + z}

where

1+z=1/a(t)1 + z = 1/a(t)1 + z = 1/a(t)

is the redshift factor.[^9] In our model, the faster flow of time increases the intrinsic rate.

Define

k(r)=1+g(r)k(r) = \sqrt{1 + g(r)}k(r) = \sqrt{1 + g(r)}

as the time acceleration factor. The intrinsic rate becomes:

Rintrinsic=k(r)RstandardR_{\text{intrinsic}} = k(r) R_{\text{standard}}R_{\text{intrinsic}} =

k(r) R_{\text{standard}}

where

RstandardR_{\text{standard}}R_{\text{standard}}

is the rate in standard cosmology. The observed rate is then:

Robs=k(r)Rstandard1+zR_{\text{obs}} = \frac{k(r) R_{\text{standard}}}{1 + z}R_{\text{obs}}

= \frac{k(r) R_{\text{standard}}}{1 + z}

For high ( z ) (large ( r )), if

k(r)>1+zk(r) > 1 + zk(r) > 1 + z

,

RobsR_{\text{obs}}R_{\text{obs}}

exceeds the standard prediction, resulting in more supernova discharges per observed time

interval compared to closer galaxies.

Observational Signature

Type Ia supernova light curves offer a precise test. In standard cosmology, their duration is

stretched by

1+z1 + z1 + z

.[^10] In our model, the intrinsic duration is shortened by ( k(r) ), yielding an observed

duration:

Δtobs=Δτk(r)(1+z)\Delta t_{\text{obs}} = \frac{\Delta \tau}{k(r)} (1 + z)\Delta t_{\text{obs}}

= \frac{\Delta \tau}{k(r)} (1 + z)

where

Δτ\Delta \tau\Delta \tau

is the standard rest-frame duration. If ( k(r) ) is large,

Δtobs\Delta t_{\text{obs}}\Delta t_{\text{obs}}

may be shorter than expected, and the frequency of events higher, detectable in JWST or

future surveys.

Discussion

This model challenges the homogeneity of the FLRW framework, positing a universe with

density gradients that affect time flow. While cosmic microwave background data support

large-scale isotropy,[^11] localized inhomogeneities could exist at high redshifts. The theory’s

reliance on an "edge" requires reconciliation with observations suggesting a boundary-less

universe, possibly by redefining the edge as regions of extreme low density.

Future observations, such as detailed supernova surveys at

z>10z > 10z > 10

, could validate or refute this hypothesis. Deviations in light curve durations or event rates

from standard predictions would signal a need to reconsider the nature of time in cosmology.

Conclusion

We propose that time flows faster near the edge of the universe, driven by reduced mass

density, offering a solution to the early galaxy formation puzzle observed by JWST. Our

modified metric enhances the evolutionary timeline of distant regions, with testable

implications for supernova rates. This work invites further exploration into the interplay of

time, gravity, and cosmic structure.

Bibliography

[^1]: Planck Collaboration. "Planck 2018 Results. VI. Cosmological Parameters." Astronomy &

Astrophysics 641 (2020): A6.
[^2]: Carter, L. M., et al. "JWST Observations of High-Redshift Galaxies: Evidence for Early

Formation." Astrophysical Journal Letters 950, no. 1 (2023): L12.
[^3]: Einstein, Albert. "The Foundation of the General Theory of Relativity." Annalen der

Physik 49 (1916): 769-822.
[^4]: Misner, Charles W., Kip S. Thorne, and John A. Wheeler. Gravitation. San Francisco: W.

H. Freeman, 1973.
[^5]: Friedmann, Alexander. "On the Curvature of Space." Zeitschrift für Physik 10 (1922):

377-386.
[^6]: Lemaître, Georges. "The Expanding Universe." Monthly Notices of the Royal

Astronomical Society 91 (1931): 483-490.
[^7]: Springel, Volker, et al. "Simulations of the Formation, Evolution and Clustering of

Galaxies and Quasars." Nature 435 (2005): 629-636.
[^8]: Nguyen, T. H., et al. "Metallicity and Mass Estimates of JWST Galaxies at z > 10."

Astrophysical Journal 955, no. 2 (2023): 78.
[^9]: Perlmutter, Saul, et al. "Measurements of Omega and Lambda from 42 High-Redshift

Supernovae." Astrophysical Journal 517, no. 2 (1999): 565-586.
[^10]: Riess, Adam G., et al. "Observational Evidence from Supernovae for an Accelerating

Universe." Astronomical Journal 116, no. 3 (1998): 1009-1038.
[^11]: Bennett, Charles L., et al. "Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP)

Observations." Astrophysical Journal Supplement Series 208, no. 2 (2013): 20.